Приведенная ниже задача интересна тем, насколько бесшовно ее кажущаяся хардкорность преобразуется в конкретные закономерности реального мира. Если первая и вторая часть вас напрягают, то лучше начните сразу с третьей.
Формулировка задачи
Канторово множество $K$ определяется так: делим отрезок $[0,1]$ на три равные части и выбрасываем средний интервал $(\frac{1}{3},\frac{2}{3})$. Оставшиеся два отрезка $[0,\frac{1}{3}]$ и $[\frac{2}{3},1]$ опять делятся на три равные части, и средние интервалы выбрасываются, и т.д. до бесконечности. Оставшееся множество и есть канторово множество. Доказать:
А. $K$ нигде не плотно, т.е., любой интервал $(α,β)⊂[0,1]$ содержит подинтервал $(α_1,β_1)$, свободный от точек $K$,
Б. $K$ несчетно (имеет мощность континуума),
В. $K$ имеет меру 0.
Решение
А. Любой подинтервал $[0,1]$ либо полностью принадлежит отброшенной области, либо содержит в себе подинтервал, который на некотором шаге $k$ построения множества $K$ был отрезком. Но тогда часть этого отрезка была отброшена на шаге $k+1$, следовательно, исходный подинтервал содержит подинтервал, свободный от точек $K$.
Б. Представим точки отрезка $[0,1]$ в троичной системе счисления: $a∈[0,1]$, $a=0.α_1α_2α_3$ и т.д., где $α_k∈{0,1,2}$. Согласно алгоритму построения Канторова множества, на k-м шаге из $K$ исключаются точки, у которых $α_k=1$. Оставшиеся точки можно сопоставить двоичным разложениям всех точек отрезка $[0,1]$ (с заменой 2 на 1), причем такое отображение является биекцией. Это значит, что мощность множества $K$ равно мощности $[0,1]$, т.е. континууму.
В. Вычислим суммарную меру интервалов, которые исключаются при построении канторового множества. На n-м шаге исключается $2^{n-1}$ интервалов длины $\displaystyle\frac{1}{3^n}$. Сложив их все, получим $\displaystyle\sum_{n=1}^{\infty}\displaystyle\frac{2^{n-1}}{3^n}=\displaystyle\frac{1}{2}\sum_{n=1}^{\infty}\Big(\displaystyle\frac{2}{3}\Big)^n=\displaystyle\frac{1}{2}\times2=1$. Вычтя это из длины отрезка $[0,1]$, получим 0 — меру канторового множества.
Научно-популярное объяснение
Ниже приведена иллюстрация процесса построения канторова множества. Ничего не напоминает?

Попробуем согнуть каждую из горизонтальных линий и присоединить ее концы к серединам линий на уровне ниже.
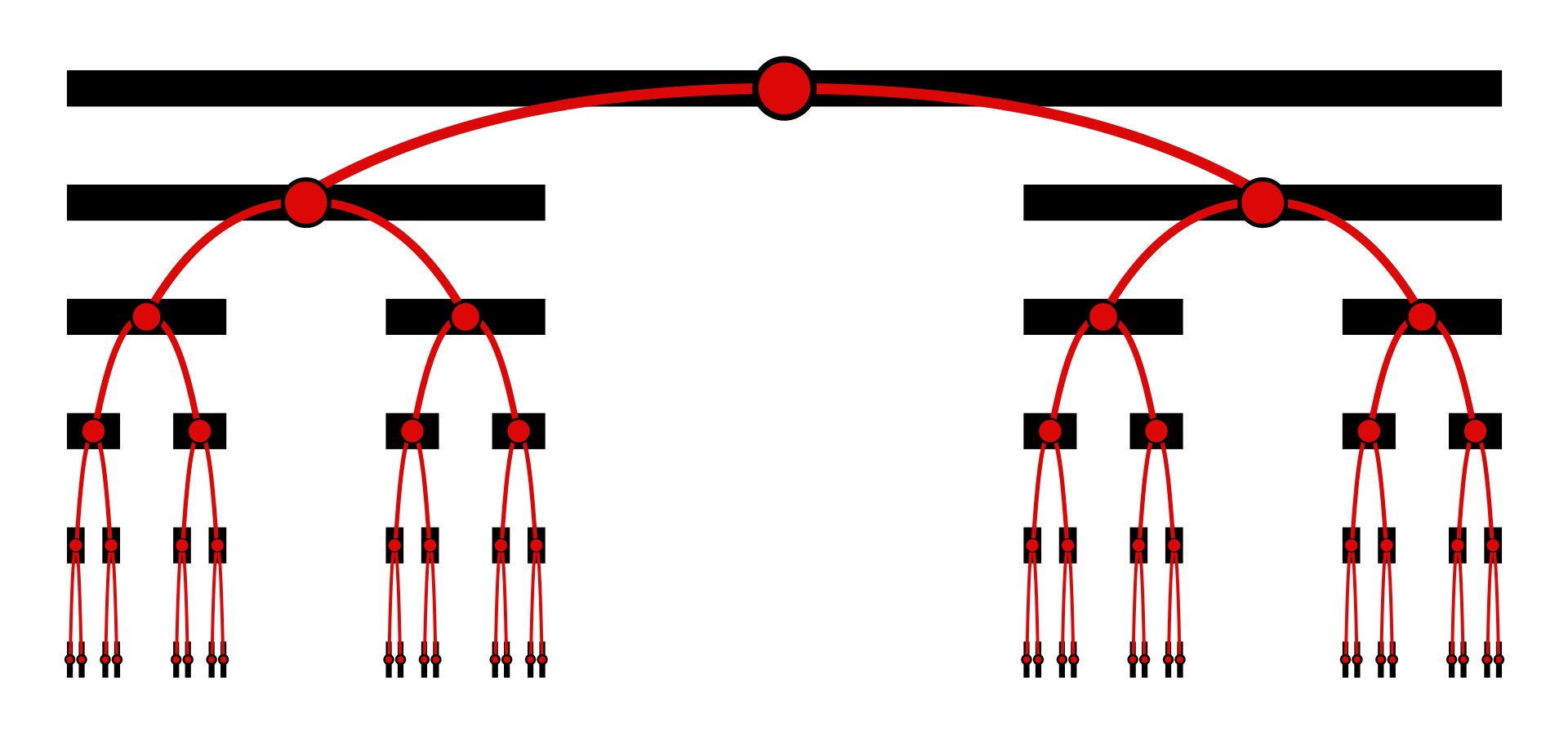
Получаем другую знакомую структуру — бинарное дерево. Кстати, почему она так называется?
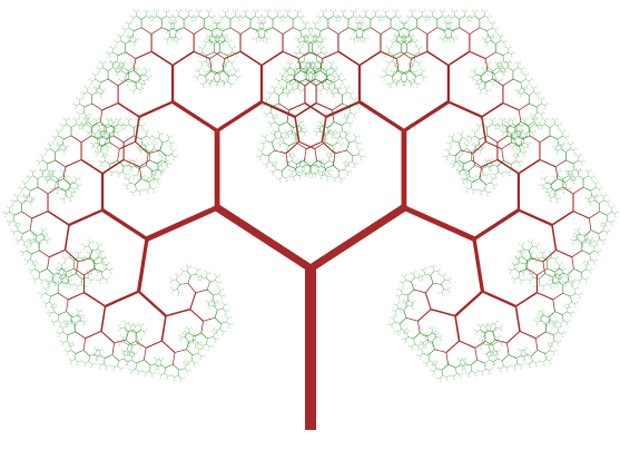
Если отрезать у настоящего дерева ветку (пожалуйста, не делайте так на самом деле), она будет напоминать уменьшенное исходное дерево. То же можно сделать и с бинарным деревом. Структуры, обладающие таким свойством, называются фракталами. А канторово множество — простейший одномерный пример фрактала.

Деревья напоминают фракталы не только ветвями, но и корнями. И вообще, в природе фракталы встречаются повсеместно. Например, наши кровеносная и нервная системы, а также легкие, имеют фрактальную структуру. Аналогично с внешними жабрами и фильтрами различных водных существ. В древних докембрийских морях существовала целая группа полностью фрактальных животных — рангеоморфов. В неживой природе те же свойства имеют снежинки и многие другие кристаллы. И в некоторой степени то же можно сказать о любой человеческой инфраструктуре — дорогах, электрической сети, Интернете.
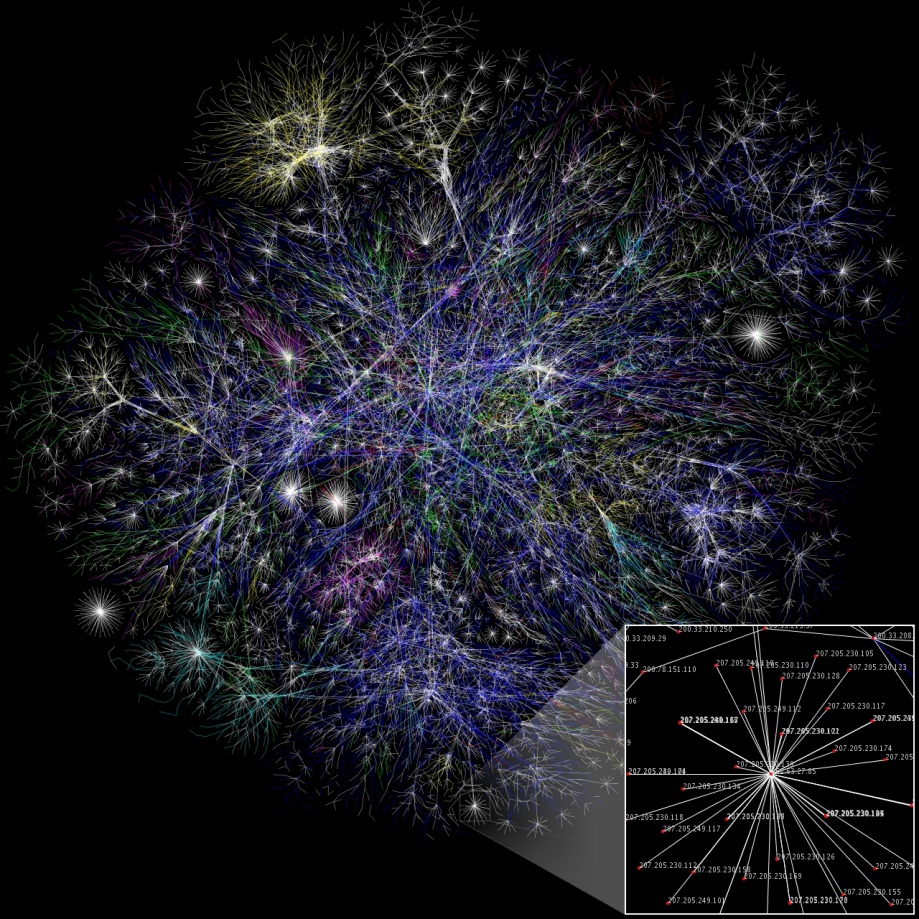
Общие свойства столь разных систем объясняются схожестью их назначения. Листья дерева должны одновременно иметь доступ к свету, воздуху и воде, поднимающейся из корней. Корни должны касаться как можно большего количества почвы, чтобы быстрее впитывать из нее воду. Кровеносные сосуды должны доставлять кровь к каждой клетке. Легкие и жабры должны максимизировать поверхность соприкосновения сосудов и воздуха, и так далее.

Общий принцип уже должен быть понятен. Фрактальная структура возникает там, где требуется максимизировать поверхность (если мы говорим о трехмерной структуре) соприкосновения двух сред. По сути, именно об этом говорит доказанное выше свойство А: рядом с любой точкой фрактала найдется точка, не принадлежащая ему. Конечно, в реальном мире эти точки не могут быть бесконечно малыми, но с описанием макроскопических структур модель фрактала справляется.
Кроме того, по свойству В фрактал имеет нулевую меру. В реальном мире это означает, что он минимизирует собственный объем, а значит, и количество ресурсов, затрачиваемое на постройку фрактальных структур. Именно этого мы хотим от инфраструктуры: она должна занимать как можно меньше места, расходовать как можно меньше ресурсов, и при этом соединять как можно больше точек.
Наконец, интересный факт: если бы можно было расплести все сосуды кровеносной системы человека и выложить их в одну линию, ее длина составила бы до 100000 километров! Для периферийных нервов эта цифра меньше, но все равно существенна: 75 километров. Таким образом проявляется свойство Б, насколько ему это позволяют ограничения реального мира.