Embeddings, Aufhebung & Denkökonomie

The problem with the contemporary discourse around AI is that there's a near-zero intersection between those who have been trying to analytically understand intelligence for millennia and those who went the "reverse-engineering" route. And the results are absolutely comical on both sides.

Machine learning perspective

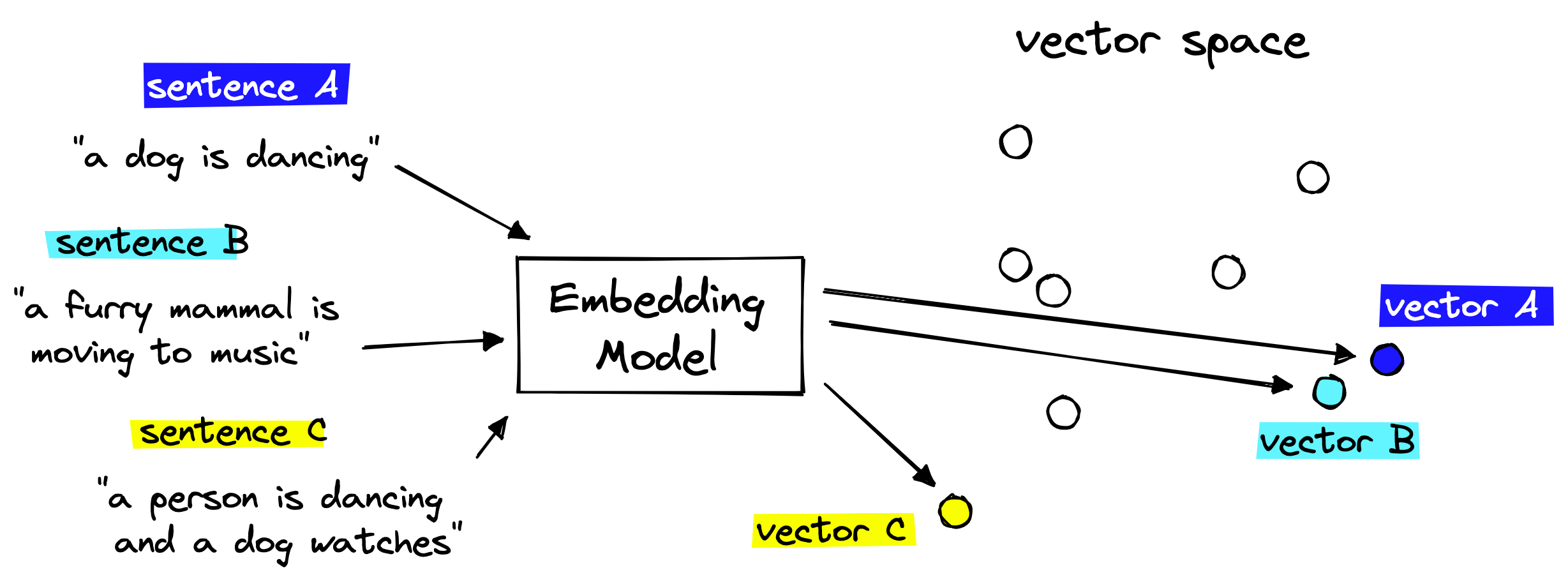
Without knowing anything about the nature of colors, we may naively assume that each hue (red, green, blue, yellow, purple, etc.) exists independently of the others. However, having started mixing colors, we quickly (or not so quickly) come to the conclusion that there are only three truly independent colors: red, green, and blue, and all the rest are their linear combinations¹ (mixtures in different proportions).

Even for those with little knowledge of mathematics, it should not be difficult to imagine colors as three-dimensional vectors (lists of three numbers). But what is the benefit of this representation? Firstly, we obtain a correspondence between the physical process of color mixing and arithmetic operations on vectors. Secondly, this representation is also maximally compressed; it takes up the minimum possible amount of memory.

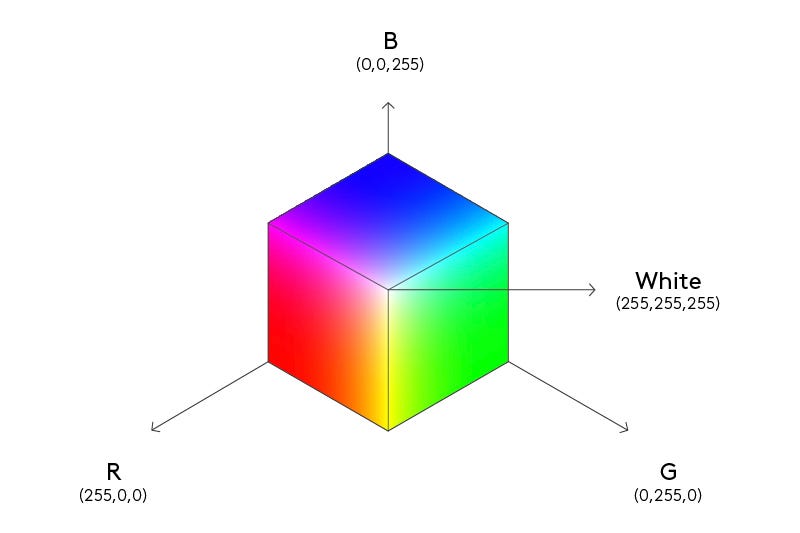
The example of colors is good precisely because we know the answer in advance. But there are many other classes of objects for which we would like to obtain a representation with similar properties, but how to do this is not at all obvious. One such class could be words.

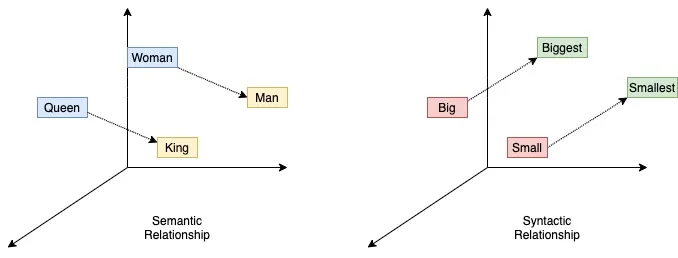
Again, we can start with the assumption that all words are independent of each other; that is, in the linear space of words, each of them corresponds to its own dimension (this approach is called one-hot encoding). But this assumption will quickly be shattered by fairly obvious examples of antonyms, such as “high - low,” “bright - dim,” “help - hinder,” “loud - quiet.” For each pair of antonyms, we can write down an equation of the form “high + low = 0”, “help + hinder = 0”, etc. In this way, we algebraically express one word through another, which means we can eliminate one of the two dimensions originally allocated to them. Moreover, the right side of these equations needs not be zero. It could also be a non-zero vector: another word. For example: “damp + cold = dank”, “irony + mockery = sarcasm”, “music + poetry = song”. Moving up a level to four words in one equation, we can begin to illustrate the different kinds of relationships between words. For example, “king - man + woman = queen” is a semantic relationship, and “big + less = small + more” is a syntactic one. These are just the simplest examples; there is no limit to the complexity of such constructs.

The problem is that considering all possible verbal equations for expressing words through each other and determining the relative positions of their corresponding vectors is a task that is far beyond reasonable in terms of labor intensity. Which is why it was solved only with the advent of machine learning. A breakthrough in word vectorization was the simply named word2vec algorithm, published a decade ago. The general public probably remembers it from some meme-worthy examples of verbal equations:

pig - oink + Santa = HO HO HO
pig - oink + Woody Woodpecker = Yabba dabba doo
pig - oink + Fred Flinstone = wassup
pig - oink + Homer Simpson = D’oh
pig - oink + Donald Trump = YOU’RE FIRED
pig - oink + Einstein = E = mc2

Along with machine learning, a new word has appeared to describe such vector representations of objects: embeddings, also known as latent vectors, since the linear space they occupy is called latent space.

The algorithm for generating embeddings turned out to be rather indirect. It consists of training a model, usually a neural network, to guess information. For example, in the case of words, we can remove one word from a sentence and have the model predict what should be in its place. Embeddings are generated during the training process as the model’s internal representations of the data that it is processing. If this explanation was confusing, then you only have to remember one thing: the connection between embeddings and predictions. We will need this connection soon.

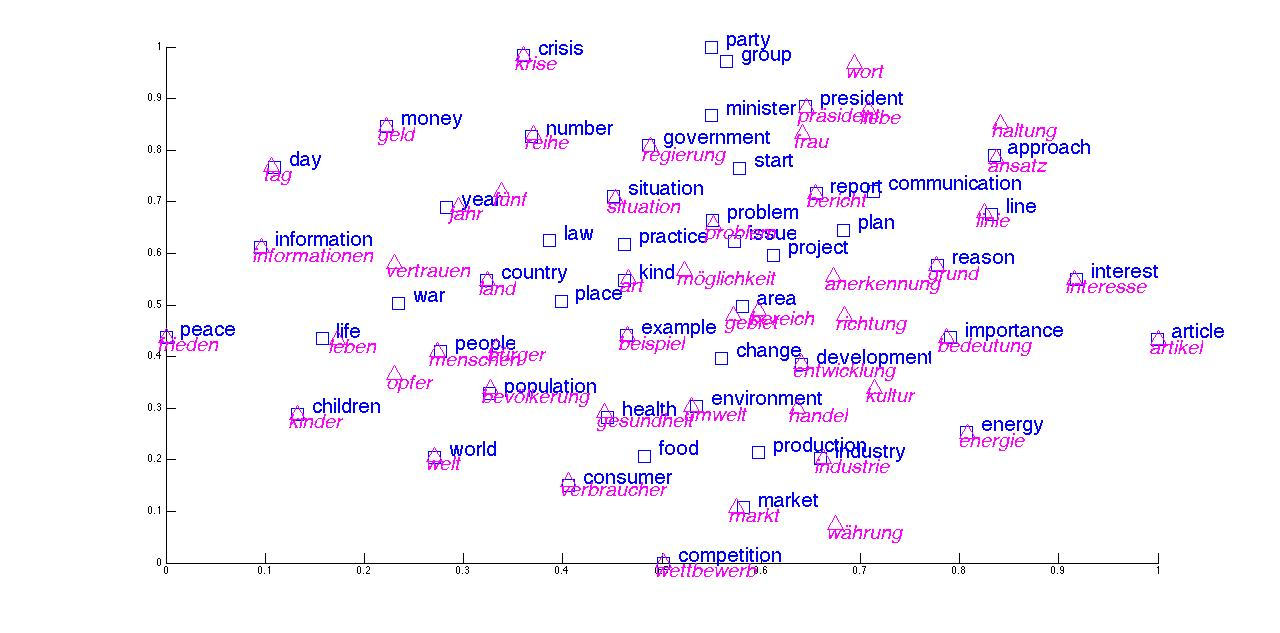
An interesting property of language is that embeddings of words from different languages will form a very similar structure, and by overlaying the latent spaces of different languages, one can create a dictionary for translation between them without a single example of actual translation. This property has been known for a long time, albeit in a different formulation, and was used by archaeologists to decipher dead languages long before machine learning. It indicates that embeddings are not arbitrary but are an objective property (or rather, a homomorphic image) of what they are encoding. So, in the limit, different methods for calculating embeddings of the same objects should theoretically converge to similar results.

With the help of machine learning, we can calculate embeddings for anything, provided that we have a sufficient number of examples illustrating relationships between the objects in question. For example, texts can be used to construct word embeddings, but you can also embed higher-level structures: sentences, paragraphs, and entire articles. They will simply require many more examples. Images are a little more complicated, but if you've ever solved a captcha like "select all squares that contain X to prove you're not a robot", you've helped some corporation (most likely Google) create better image embeddings.

Embedding technology is also a pillar of all breakthroughs in the field of artificial intelligence in recent years, which is not surprising: embeddings, in essence, are a portal between the real world of people and the digital world of machines. ChatGPT and other generative neural networks like Stable diffusion and Midjourney rely on them.

And speaking of image-generating models, have you ever seen videos that consist of images endlessly morphing into each other, often in disturbing ways? It is also possible to specify a starting and a final image, and a model will interpolate an uncannily smooth transition between them, no matter how different they are. The fact that this is possible means that there is a nearly infinite number of images in between any two. This notion of something being between two images is the key to understanding the nature and limitations of creativity that contemporary generative AI exhibits.

Because, large as it may be, the latent space mathematically cannot contain all possible images or texts: their numbers are many orders of magnitude higher, and the vast majority are just noise anyway. So, what does it contain? It includes all possible things you can get by recombining the pre-existing data in various ways. All possible results of such recombinations taken together are called the span.

So then, what makes the creativity of GenAI different from that of humans? GenAI is locked within the span of the data it was trained on. This span is mindbogglingly large and has enough samples that will appear original to us. On the other hand, not all human artwork is original either: most of it is also a remix of what came before. But a human can, at least in principle, create something outside this span. If this weren't the case, it would be impossible for human creativity ever to begin because there would be no initial span for the very first artists or writers to sample from.

Of course, modern GenAI does much more than walk across the latent space: LLMs answer your questions, and image generation models create pictures from a textual description. But these abilities really just come down to doing fancier math in the latent space to find what the user is looking for more efficiently. The fundamental limit on GenAI creativity remains the same and will remain the same until we come up with a completely new technological paradigm for AI.

The problem is that there is not even a universally accepted explanation for why the paradigm we currently have is working to the extent it does. However, one explanation that I personally subscribe to is the Manifold hypothesis.

The simplest example of a (low-dimensional) manifold is a sphere. While the sphere itself is a 3D object, its surface is 2D, meaning that we can uniquely identify any point on it with only two numbers. And even if we are only given 3-dimensional vectors describing points on this sphere, given enough of them, we should be able to reconstruct the complete sphere and remap them to the two-dimensional surface.

What the manifold hypothesis posits is that deep learning is doing exactly that. First, it assumes that all naturally occurring and useful data intrinsically exist on low-dimensional manifolds inside the spaces where we find them: for example, meaningful sentences are a manifold within the space of all possible strings, and images we can recognize as pictures are a manifold within all possible combinations of pixels. The task of the neural network is then to find these manifolds and flatten them into linear spaces, which we already know as latent spaces. In fact, the extracted and flattened manifold is nothing else than the already familiar span, and the data points remapped to it are nothing else than embeddings.

Applications and implications

By formal definition, embeddings are just vectors whose geometric distance is proportional to the similarity of the objects they represent (an isometric homomorphism, if you will). Essentially, computing embeddings is the task of classifying objects and determining their degree of relatedness, whatever that means in each specific case.

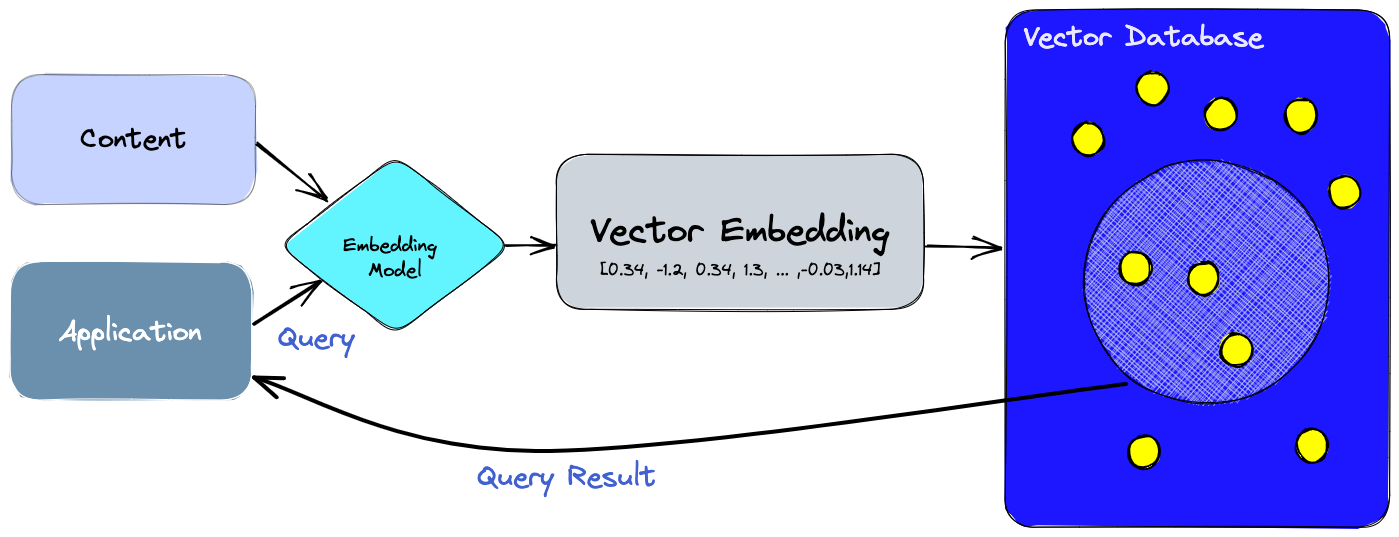
This property of correspondence between geometrical distance in latent space and similarity of embedded objects can be leveraged to perform similarity search. First, you build a database of embeddings (called a vector database) as a key-value storage, with vectors being keys and original objects being values. Then, you can run any new object through the same model to obtain its embedding. Finally, you do a K-nearest-neighbors search on that embedding in the database and return the values corresponding to found keys. This is roughly how image search, facial recognition, and recommendation algorithms work. Even most text search engines already use embeddings to search not only for literal matches with the search query but also for texts that are similar in meaning but phrased differently. Such search is called semantic.

But, as I briefly mentioned at the beginning, a side effect of computing embeddings is the compression of information². And there is some reason to believe that this is not just a side effect but an equivalent definition of embeddings. This reason is an incredibly interesting article, which proposes a way to measure distance between texts using compression (based on the notion of Kolmogorov complexity), thereby allowing the use of compressed texts as quasi-embeddings. It then compares embeddings produced by the most powerful language models with a conventional Gzip archiver in the text classification task. Paradoxically, in many tests (especially on small samples and outside the training distribution), Gzip's performance came close to much more complex language models.

If that made no sense to you, then here is the conclusion in simpler words. Classifying objects requires identifying their common features, but if we have found such features, then we no longer need to remember them for each object separately; it is enough to have one record for all objects of the same class. Conversely, the task of information compression requires a reduction of repeating sequences, which turn out to be common properties of objects. In other words, both tasks come down to generalization.

But notice that neither machine learning nor even embeddings themselves appear in the previous paragraph. This is because it uncovers a much more general principle that applies, among other things, to the human brain. Evidence of this can be found in research from the field of mind reading: this year alone, two sci-fi-level results were obtained there.

The first is the semantic reconstruction of language: decoding heard, read, and even imaginary (internal) speech from brain scans. Remarkably, the developed system does not reproduce words exactly but in a slightly different formulation that preserves the general meaning, hence the “semantic” qualifier. This means that it reconstructs the thoughts themselves and not, for example, the motor signals that the brain involuntarily sends to the tongue and larynx, even when it is not speaking out loud. But most interestingly, if the same system is used on a person who is watching a silent film, the result of decoding their thoughts will be a text description of the scenes of this film!

The second result is a similar system but for the reconstruction of images, visible or imaginary. Its properties are the same: the images do not match exactly, but they are similar in a rather curious way, reflecting what details the person is paying attention to.

Both systems share a very similar architecture and contain two key elements:

1. Generative neural network. Semantic language reconstruction uses GPT-1, and image reconstruction uses a diffusion model from the same class as Stable diffusion and Midjourney.
2. A model of the subject’s brain, implemented as an artificial neural network that, based on data (text or picture), predicts what signals the brain that thinks about this data will produce. I was amazed by the fact that this is already possible: in theory, modeling the human brain should not be achievable with the current level of technology. However, the models exist, and they work. Even if this is just a rough approximation at the moment, the very fact that such an approximation is possible and useful makes a big difference in estimating the complexity of this problem. Fortunately, to obtain results, the model must be trained individually on each subject, which is impossible without their cooperation, so it’s yet too early to worry about the adoption of mind reading by states and corporations for nefarious purposes. Yet.

The system works as follows. First, the generative neural network creates many different variations of text or images. These options are fed to the neural network that models the brain, and it generates corresponding signals. They are compared with real brain scans of the subject, and the most similar ones are selected. The data that generated these signals arrive at the output of the system as decoded results, but at the same time are transmitted back to the generative model, which generates suitable continuations to repeat the process.

All this is strikingly reminiscent of the semantic search mechanism described above. If we treat brain states as analogs of embeddings, then the process of mind decoding is just a similarity search in the space of these embeddings. Indeed, earlier studies independently confirmed that the brain also uses the concept of latent space, and the process of memory consolidation in the hippocampus is strikingly similar to the computation of embeddings. Particularly amazing is a paper showing equivalence between the hippocampus model and transformers, a class of artificial neural networks that underlie recent breakthroughs in natural language processing (that’s what T in GPT stands for) and which were developed without any prior knowledge of neurobiology. So, science once again converged to a solution that nature had already invented³. But this raises another question: what problem was nature solving?

Neurobiological perspective

On the one hand, the adaptive value of the human brain cannot be overestimated (says a human brain, ha-ha), which means that its development should have been very strongly encouraged by natural selection. This is supported by the relatively rapid evolution of the human brain. On the other hand, biophysics imposes strict constraints on the parameters of the brain. These are, firstly, physical dimensions, limited by the constraint of having to be born. Secondly, the human brain already consumes a fifth of the body’s total energy, and energy in nature is a strictly limited resource, so there was no opportunity to freely increase its consumption until quite recently, by evolutionary standards, with the emergence of agriculture. Thus, we have a very acute contradiction between the need to increase the power of the brain and the limitations on the parameters by which this could be achieved. It then follows that the evolution of the brain should have gone in the direction of increasing efficiency. And indeed, it seems that it is already about as efficient as it can theoretically be. Many other human adaptations that increase energy efficiency at the expense of brute force hint at the same direction.

But how is this efficiency achieved? For the answer, we again have to turn to machine learning, which found that if you constrain the model in the energy budget, it automatically produces a predictive coding mechanism: the same one that produces embeddings! Moreover, transferring this result from artificial neural networks to biological ones is not a leap of faith: we already know for sure that predictive coding mechanisms arise in almost any well-optimized part of the brain.

Since humans spend most of their time communicating with others (or at least did so until they invented the damned Internet), optimizing social interaction has been a high priority for evolution. The result of this optimization was, on the one hand, a highly specialized language cortex, which constantly tries to predict what it will hear, and on the other, mirror neurons, which completely model the mental state of other people (and, with proper development, not only people), and therefore they inevitably operate with compressed representations, since no system can completely model itself.

If you reflect on the subtleties of your own behavior, you may notice these systems at work every time you interact with information in any way. For example, when opening an article, you may semi-subconsciously glance at the author, and if you already know them, then your brain will quickly make a prediction of what you are going to read about using the information it remembered from previous articles by the same author. This decreases the energy required to process the text and makes the reading process less frustrating. But this may also lead you into an echo chamber.

Incidentally, the part of your brain that makes this prediction works in a way not unlike a text generation neural network such as GPT, at least on the surface level. We know for a fact that generating speech or text is handled by a different brain structure than analyzing it: Broca’s area and Wernicke’s area, respectively. This is what the famous Hemingway’s advice "write drunk, edit sober" captures. This also hints at another limitation of contemporary generative language models, as well as at how to overcome it. Instead of trying to build one model that can, so to speak, write and edit at the same time, we should mimic the brain structure and develop a different type of model that works similarly to Wernicke’s area and then connect them.

“What I cannot create, I do not understand,” said Richard Feynman. Conversely, the best way to understand something beyond any doubt is to create it. So then, isn’t the creation of artificial intelligence our most successful attempt to understand our own?

From a theoretical point of view, all this fits perfectly into the system of general theorems formulated for all systems, including brains, within the framework of cybernetics. One of these theorems states that if we consider the subject and the world with which they interact as computers exchanging information, then making optimal decisions for the subject, which is equivalent to predicting the consequences of available actions, is reducible to the maximum compression of information about the world. Of course, it would be premature to transfer this theorem to the real world since it is based on a rather shaky assumption of universal computability. But it would be equally unwise to ignore its conclusion.

And now, it's finally time to put everything together. Efficiency necessitates prediction, prediction necessitates generalization, generalization is equivalent to compression... And what is compression? It is the efficiency⁴ of storing information! The loop is closed, which means that all these processes are equivalent to each other at a fundamental level!

Philosophical perspective

The conclusion derived above is, of course, not that new. Similar ideas have been put forward in many forms, starting perhaps from an Austrian philosopher Ernst Mach and his scientific framework of Denkökonomie, which literally translates to “economy of thought”, “economy” meaning savings or efficiency. At its core, this framework demands the simplest possible (most economical) explanation of observed facts in science; it's essentially a beefed-up version of Occam's Razor, which Mach also derived from biological necessity.

But what do we mean by this complexity/economy quantitatively? One answer is explanatory power, which is expressed as a ratio of the number of observations a theory explains divided by the number of assumptions that it relies on and which are unprovable within it. This is usually enough to compare two theories within the same subject domain. In the context of statistical models, the number of assumptions can be replaced with the number of trainable parameters. But it is possible to generalize even further.

Recall the concept of Kolmogorov complexity mentioned earlier. Based on it, a theoretical measure of complexity for scientific theories was suggested by Ray Solomonoff as part of his theory of inductive inference. This is, in essence, a mathematical formalism for Mach's philosophical framework. It, in turn, is the basis for AIXI: an algorithm that is supposedly capable of discovering the most economic theories automatically; in other words, an AGI. The only issue is that none of these things are computable, which is why they were never used in practice. Some, however, try to approximate AIXI, and this avenue of research probably deserves more attention than it is currently getting.

It is easy to see that scientific progress almost always goes in the direction of more economical theories, at least when considered on a sufficiently long time scale. For example, when radioactivity was first described, it did not fit into existing physical theories at all. Initially, it had to be considered as a completely independent phenomenon, which, of course, is not economical in the short term. But new theories soon emerged, combining old physics with new phenomena into a single and more economical system, and at the same time explaining things that previously seemed inexplicable: why are stars burning, and where atoms come from. Mach himself likely developed his framework by trying to formalize this very observation.

Ironically, most people who know about Denkökonomie today know it not from the source material but from the critique of it penned by Lenin. Therefore, it wouldn’t be fair to proceed without addressing it first.

Lenin’s perspective

If we accept that (1) Denkökonomie is a sufficient criterion of truth and (2) the brain always strives for the most economical explanation of observed facts, then it follows that all people, as they gain experience, should converge on identical ideas about the world. But empirically, this obviously does not happen. This contradiction can be explained in two ways. The way that Mach chose was to deny the materiality of the world. Indeed, if each observer analyzes their own world, then there is no basis for consistency between their models of those worlds. Thus, Mach eventually reasoned himself into solipsism by an overly extreme application of his own principle.

But ironically, a much more economical way to explain the same contradiction is to abandon one of Mach's postulates. Since postulate 2 is now backed by science (as explained above), the problem is obviously in postulate 1. That is, Denkökonomie is not a sufficient but a necessary criterion of truth. Put simply, this means the truth cannot be found by following simplicity alone (string theory and supersymmetry empirically demonstrated this), but somehow, the truth always turns out to be simple.

Having asserted that, we are left with the problem of coordination between the brain and the world outside it. To fill that gap, Lenin developed the dialectical materialist reflection theory, which became the model of intelligence in Marxism. The theory of reflection by itself is much older and simpler than Marxism and, at the base level, alleges that while we can only access objective reality through sensations, the results of these sensations are normally consistent with reality itself. Were they not, there would be no adaptive value in having the sensations and they would have never evolved in the first place. In other words, we have an internal model of reality in our minds that is being constantly clarified and grounded by sensations. The process of perception is then a transformation of a thing-in-itself into a thing-for-us through reflection.

The problem is that any kind of reflection theory has a hard time explaining specifically how this process of transformation works since the thing-in-itself is obviously far more complex and detailed than the thing-for-us. The vast majority of information is necessarily lost in this process of transformation, so the question is: what is retained?

For Lenin, the answer is that the information we retain is what is useful in practice. Although usefulness is rather subjective as it heavily depends on the goal of the actor, many actors pursuing different goals eventually arrive at similar representations of the world. Thus, the process of reflection converges and becomes deterministic in the limit.

Take a map as an example. If you download a map of the greater Berlin from Google Maps, it takes up a mere 100 megabytes: less than 30 bytes per capita (what a unit, huh). In that space, Google fits pretty much all the information you will realistically need to live in the city, and yet no one would argue that it encompasses the full experience of Berlin. This trick works because society has developed many useful abstractions, such as roads and buildings, which can be represented with only a few numbers each.

And what do I need a map of Berlin for? To predict where a specific train will take me or where I will end up after turning left or right at a specific intersection. So, usefulness is essentially a proxy for predictive power, and it is also connected with compression.

But this connection goes both ways. We capture the compressible aspects of reality, but then we also use the understanding of these aspects to shape reality itself to be more compressible, like building straight roads and rectangular houses. This idea, if extrapolated, has some surprising and potentially useful implications.

A surprise detour into the Fermi paradox

Imagine we are writing software for an interstellar microprobe that will be launched to perform close-up imaging of a potentially inhabited exoplanet. Problem is, we cannot transmit the image back home for analysis: the probe has neither the antenna size nor the power budget for that. All we can send back is a single number: the probability that the planet hosts a technological civilization. How do we compute it?

Leaning on what was said in the previous section, we can assume that aliens, like us, will build regular (and therefore compressible) structures, because they, no matter who "they" are, will find regularity more useful than chaos. And, luckily for our probe's processor, this regularity can be easily measured without any assumptions about the form and function of structures on an image by simply calculating its entropy.

Long-time readers know that I've long been obsessed with the Fermi paradox, and specifically with deriving an answer to it from the definition of intelligence. In my paper on the topic I started with three different definitions and then expressed them through each other (so far only in the limit). And it is no coincidence that entropy was also the thread connecting these definitions.

But let us also consider counterarguments to my proposition, which can me made from both sides.

On the one hand, not everything that is compressible is artificial. Simple periodic patterns often occur in nature without life being involved, such as snowflakes or basalt columns. Crystals in general are great at making these and, given the right conditions, could form structures visible from space. Then there are fractals: a class of patterns that are extremely compressible and are widely used in both nature and technology.

On the other hand, the highly regular structures that we are building today require lots of effort to maintain. It is possible to imagine that, as technology evolves in the direction of self-replication and self-maintenance, technological structures become chaotic again, converging with nature. This idea has lots of potential for further development, and I hope to come back one day to give it a good think.

Platonic perspective

Slightly earlier I made an unsubstantiated claim that the category of "useful" information is, in the limit, independent of the goal for which it is used. This, if true, is a deep and fundamental conclusion about the structure of reality itself, so it requires some justification.

It is a well-known empirical fact in the deep learning community that training a model on the task you actually want to perform is not always a great start. Often it benefits to first train it on a more general task (known as pretraining) before specializing it to your specific use case (known as fine-tuning). For example, a language model that is first trained to understand multiple languages and then fine-tuned to translate between them performs much better compared to the same model trained on examples of translation from the start. And you can understand why, if you scroll back to the example of word embeddings for two languages overlayed on each other. This implies that the same representations of data are useful for many different tasks, in other words, they converge.

This convergence for language and vision models has been recently measured in an already famous paper "The Platonic Representation Hypothesis". ChatGPT-4o heavily leverages it by using the same internal representations for different data types. There are also examples of representations convergence that are much harder to comprehend, such as a model for solving partial differential equations that performs better after pretraining on... cat videos?

This is hopefully enough to show that the convergence of representations between different tasks is empirically real. On the theoretical side, the explanation of this effect is offered again by the Manifold hypothesis. If real (or useful) data always lies on low-dimensional latent manifolds, then jumping from one manifold to another (fine-tuning) will always be easier than finding the manifold in random noise, which is the alternative to pretraining.

On the philosophical side, this looks a lot like Platonic idealism, which posits the existence of Forms: ideal representations that precede and give rise to material objects. Similar ideas can be found in Eastern philosophies. While this does not imply that we need to reject materialism in favor of objective idealism, it definitely posits some questions that will be very hard to answer from the materialistic perspective. But I am sure that it will be worth it.

And if we once again allow ourselves to make analogies between neural networks and human brains, then this conclusion gives us an interesting perspective on the education system. I often hear people complaining about learning trigonometry in school, which no one ever uses after graduation. And fair enough, even I, a professional mathematician, rarely use it (and certainly look up trig identities instead of trying to dig them from the depth of memory). What is the point of learning such seemingly useless things? Could this be a form of pretraining that helps in life later in ways we do not consciously recognize? I suspect so, because people who did not graduate school empirically end up performing worse in a wide range of tasks, meaning that the school definitely does something useful. We just don't have the language to explain what remains in the head of an educated person after all the trig identities, poems and historical dates are no longer there.

Copernican perspective

I must add, however, that there are situations where Denkökonomie can be used as a criterion of truth, namely, all else being equal. For example, if we put ourselves in the shoes of people who do not yet know about Newton's theory of universal gravitation, then how should we choose between the geocentric and heliocentric cosmological models? Both give fairly accurate predictions, so it is impossible to reject one of them by experiment alone. What is the difference between them? The heliocentric model uses a fixed and small number of parameters to describe orbits, while the geocentric model, in order to achieve the same accuracy, requires winding epicycles onto epicycles, thereby generating many more parameters. Later, Joseph Fourier invented one of the most powerful tools of mathematics: the Fourier transform, which allows one to describe any trajectory or signal in a similar way. Hence, the geocentric model is bad not because it is incorrect but because it does not actually contain information about the motion of the planets: all this information is stored in its parameters. The heliocentric model compresses this information, saving parameters, and this is what makes it preferable. In other words, the heliocentric model has greater explanatory power.

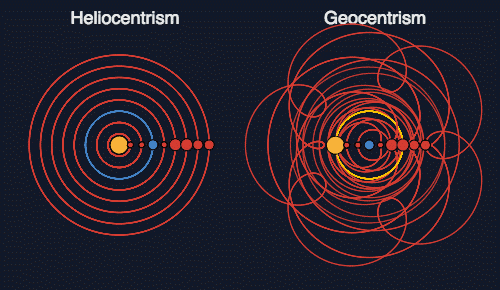
While we should strive to use “Copernican modeling” wherever possible, there are problems where this approach fails, and we are forced to resort to “Ptolemaic modeling.” Statistics and machine learning are essentially sciences that study how to do it properly.

The price for using over-parametrized modeling is usually the model's inability to generalize. In order to at least somewhat regain it, regularization and dimensionality reduction methods were invented. They can be described as artificially limiting the complexity of the model in terms of the number of parameters or their values, in essence, forcing the model to be more economical. These methods come dangerously close to using Denkökonomie as a sufficient criterion of truth, but practice shows that they work, and it is practice that is the ultimate criterion of truth.

Hegelian perspective

But let us return to the contradiction in Mach's philosophy. Even having rejected Denkökonomie as a sufficient criterion of truth, we are still left with the question: why do different people come to completely different ideas about the world if its economical (compressed) representation, which the brain seeks to find, must be objective and independent of the observer? To answer this, we will have to turn to another branch of philosophy: dialectics.

What we need from dialectics specifically is the concept of “Aufhebung,” which I will translate as “overcoming,” although no perfect translation to English exists. A classic example that demonstrates this concept is found in the relationship of the general theory of relativity and quantum mechanics with classical mechanics. These more advanced theories extend beyond classical mechanics, yet they also preserve it as a special case in the limit: when the speed of light approaches infinity and the Planck constant approaches zero, respectively. Technically, we can say that these theories are contradictory because, empirically, the speed of light is not infinite, and Planck's constant is not zero. However, the important thing is that more advanced theories can usually simulate less advanced ones through similar thought experiments.

The procedure of dialectical overcoming is invaluable in theoretical disputes, where the opponent will always present facts that do not fit into your theory. If you cannot use it, you will eventually find yourself sandwiched between two losing options: challenging the facts and removing the facts from the scope of your theory. But the ability to overcome such contradictions not only allows you not to lose an argument but also turns the dispute into a full-fledged research activity that can potentially lead to new discoveries. In such a dispute, truth can really be born.

However, the easiest way to trace the process of dialectical overcoming is not in discussions between different people but in the process of development of a single person: oneself. Each of us, in the depths of our closets or hard drives, has some notes from ancient times, looking at which we can die of cringe understand how our worldview developed. And the basic law of this development is the preservation of previous versions of ourselves that we overcame. We never throw away all previous experience to start from scratch. Even when radically changing our views, in the new ones, we retain an imprint of the old ones, which strengthens them. For example, it allows us to argue for the new worldview much more competently compared to those for whom it is the starting point. The same logic explains the antifragility of the human mind: it is by overcoming (in a dialectical sense) pain and hardship that we become better as people. And I also believe that somewhere here lies the answer to the problem of continual learning, but extracting it will take some more work.

For the same reason, not a single generally accepted theory in modern positive science can be refuted. The only way to advance further in knowledge is to overcome the old theory, that is, to find a more general theory, a special case of which will be the old one. But since generalization, as we found out above, is equivalent to compression, it turns out that the result of dialectical overcoming should be more economical. And since dialectical overcoming is also a process of removing contradictions, the converse proposition can be formulated: the more economical our theories are, the fewer contradictions there are between them.

The same logic explains why persuading people generally doesn't work. It is impossible to produce an “embedding” that can natively integrate into another person's “latent space” without access to their subjective experience, which is inaccessible to us by definition. Only I myself can convince myself of something, either in order to resolve the contradiction in my current model of reality or under the influence of material factors. Socrates’ “maeutics” is based on the first option: it consists of identifying contradictions in the interlocutor’s worldview and making them obvious. Sometimes, this leads to the interlocutor reflecting and changing their opinion in order to resolve the contradiction. However, it is impossible to guarantee persuasion, let alone in a specific direction. Socrates was fine with that: in his gnoseology, each person already contained true knowledge about the world a priori, and all he had to do was to extract it. But that view leads to the same dead end in which Mach later ended up.

Another significant drawback to this architecture is that it’s monolithic, meaning that it’s impossible to transfer a part of knowledge from one model to another. Returning to the example of embeddings, we can see a manifestation of this problem in that the embeddings themselves are useless without the model that generated them. For the same reason, it is impossible to simply “download” the knowledge accumulated by humanity into the brain of an individual person. Each brain is a new model, and each must independently build its “latent space” from scratch. For this, it must conceptually go through the path that its predecessors already took (this is indirectly confirmed by the above studies on mind reading, where a model must be fitted to each subject). The development of a person repeats in miniature the development of the entire civilization in which they happened to be born. This, by the way, imposes an unpleasant limitation on science itself: sooner or later, the time required to retrace the path of humanity, even in its most compressed form, will exceed life expectancy, and new generations simply will not have enough time to create something original; therefore, artificial life extension or other ways of overcoming this limitation (e.g., hiveminds) will become a necessary condition of further progress. But today may be too early to worry about it.

The dialectical discussion method

After reading all of the above, I bet you’d never guess what question prompted all of this research. That question was: how do we hold discussions on complex topics and reach useful outcomes at their end? I will call this "the dialectical discussion method" since this name seems unoccupied and formulate it as a set of rules.

The first rule of dialectical discussion is never to assume that any party in an argument can be absolutely right or wrong. In dialectical terms, "everyone is a bearer of a relative truth." In general, each person develops a model of reality that explains their subjective experience, and this experience, in turn, reflects only a very limited patch of objective reality. Such limited models may well be internally consistent but, at the same time, mutually exclusive. All existing discussion methods are useless in such a situation: the interlocutors cannot accuse each other of contradictory beliefs, yet at the same time, they cannot find any common ground on which some kind of compromise could be built.

And here, a previously derived conjecture comes to the rescue: "The more economical our theories are, the fewer contradictions there are between them." In terms of models and dialectics, it can be rephrased as follows: the dimensionality of the model that overcomes the contradiction is smaller than the dimensionality of the contradictory models. The last time we talked about dimensionality was in the context of regularization. And this leads us to the second rule of dialectical discussion: regularization of theses. By analogy with machine learning, we have two complementary ways of implementing it:

1. The first, analogous to the dimensionality reduction, is the removal of redundant concepts. Before proceeding to the logical analysis of the theses, it is necessary, within reason, to minimize the number of concepts used in the theses of both interlocutors by expressing some concepts through others. This will also help ensure that participants understand all the concepts being used. The best-case scenario also includes the introduction of new concepts that generalize others and reframe the contradiction in such a way that a solution to it becomes self-evident.
2. The second, similar way, roughly corresponds to Sagan's rule: "Extraordinary conditions require extraordinary evidence."

Finally, the third rule of dialectical discussion, inextricably linked with the second, can be formulated as follows: "At each stage of the discussion, there must be an opportunity for an external observer to enter into it, without studying the entire conversation as a prerequisite." At first glance, this rule may sound arbitrary, but in fact, it is nothing more than an adaptation of a famous maxim that often emerges in the positive sciences:

A mathematical theory is not to be considered complete until you have made it so clear that you can explain it to the first man whom you meet on the street.

— David Hilbert

The same idea has been formulated many times by scientists in various ways. I will not miss the opportunity to recommend once again Feynman's essay "Is Electricity Fire?" from the book "Surely You're Joking, Mr. Feynman!". It describes the likely origins of this maxim: when discussions are held in a "closed space," they tend to accumulate a hidden structure, which the interlocutors themselves are not aware of but which prevents them from arriving at the right answers. This can be counteracted in different ways. The best case scenario is when the participants themselves hold models of that "first man whom you meet on the street" in their heads and constantly explain their theses to this model, a kind of advanced self-criticism. In the general case, though, we should not count on this, so criticism should come from outside. One option is to actually bring new people into the discussion at every turn and force the discussants to involve them in the course of things. Alternatively, they could compile summaries/digests of their theses and publish them in the public domain.

At the moment, the rules of dialectical discussion are purely theoretical in nature. Therefore, the next step is to test them in the field.