Введение

12 апреля 2016 года знаменитый британский физик Стивен Хокинг и российский бизнесмен Юрий Мильнер объявили о выделении $100 млн на финансирование проекта Breakthrough Starshot. Целью проекта стала разработка технологий для создания космических аппаратов, способных совершить межзвездный полет к Альфе Центавра.

Основой проекта Breakthrough Starshot стала статья профессора физики Калифорнийского университета в Санта-Барбаре Филиппа Любина «План для межзвездных полетов» (A Roadmap to Interstellar Flight). Основная заявленная цель проекта состоит в том, чтобы сделать межзвездные полеты возможными уже при жизни следующего поколения людей, то есть не через столетия, а через десятилетия.

Межзвездный зонд будет представлять собой космический парусник с электронным модулем StarChip массой 1 г, соединенным сверхпрочными стропами с солнечным парусом площадью 16 м^2, толщиной 100 нм и массой 1 г. Конечно, света нашего Солнца недостаточно, чтобы разогнать даже столь легкую конструкцию до скоростей, при которых межзвездные путешествия не будут длиться тысячелетиями. Поэтому главная идея проекта StarShot — это разгон с помощью мощного лазерного излучения, которое фокусируется на парусе. По расчетам разработчиков, полет к Альфе Центавра продлится около 20 лет.

Цель данной работы — моделирование описанной системы и оценка достижимости фантастического заявленного срока в 20 лет.

Описание модели

Постановка задачи

Космический зонд состоит из полезной нагрузки и фотонного паруса с фиксированными размерами и массой. Для его разгона используется фазированная решетка лазеров, имеющих фиксированную мощность и длину волны, сфокусированных на оптической бесконечности.

Упрощающие предположения

• Влияние атмосферы Земли на луч лазера не учитываются. В реальности выполнения этого условия можно добиться, расположив лазер не на Земле, а на ее орбите или на Луне.
• Дифракционное рассеивание лазера описывается моделью Гауссового луча.
• Фотонный парус зонда является идеальным отражателем.
• Система прицеливания лазера идеальна: он все время направлен на центр паруса зонда перпендикулярно ему (т.е. движение небесного тела, на котором расположен лазер, также не учитывается).

Выбор переменных и констант

Заявленные параметры системы (в данной работе не оценивается их практическая достижимость):

W = 10^11 Вт — суммарная мощность лазера
σ = 6.2E-5 — поверхностная плотность паруса
S = 16 м^2 — площадь паруса
m0 = 1 г — масса полезной нагрузки

Параметры, значения которых предполагаются из общефизических соображений:

A = 1 км — апертура лазера. Такое значение невообразимо для лазера классической конструкции, но вполне достижимо для фазированной решетки.
λ = 0.5 μм — длина волны лазера, выбрана на нижней границе полосы пропускания атмосферы Земли.
T_end — время работы лазера, является параметром модели.

Общеизвестные константы: скорость света c и расстояние от Альфы Центавра D.

Внутренние переменные:

l(t) — расстояние между лазером и зондом в момент времени t, м
p(t) — импульс зонда относительно лазера в момент времени t, кг⋅м/с
M = m0 + σS — полная масса зонда, кг
θ — угол дифракционного расхождения луча, рад.
B(l,θ) — площадь, по которой распределяется энергия лазера на расстоянии l от источника, м^2

В качестве выходного значения мы хотим получить время полета до Альфы Центавра.

Теоретическая часть

Поскольку заявленная максимальная скорость зонда составляет около 20% от скорости света, для описания его движения необходимо использовать релятивистскую механику. Составим уравнение для p(t):

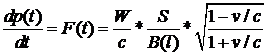
В правой части первый множитель — максимальная сила давления излучения, второй — доля энергии лазера, которая попадает на парус зонда, третий — поправка на эффект Доплера. В уравнении присутствуют две переменные: v и l. Первая однозначно выражается через p(t), но вторая является независимой и требует дополнительного уравнения. Из релятивистской зависимости между скоростью и импульсом получаем:

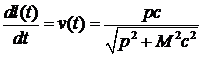
B(l,θ) — площадь основания усеченного конуса с углом наклона сторон θ и высотой l. Она легко выражается геометрически:

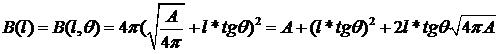
При больших значениях l можно отбросить линейную часть функции:

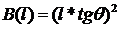
Угол дифракционного расхождения в модели Гауссового луча — константа, равная

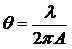
Объединив все это, получаем систему ОДУ с двумя неизвестными:

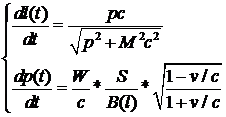
Зная импульс (и, следовательно, скорость) зонда в момент выключения лазера, легко найти время в пути до Альфы Центавра.

Практическая часть

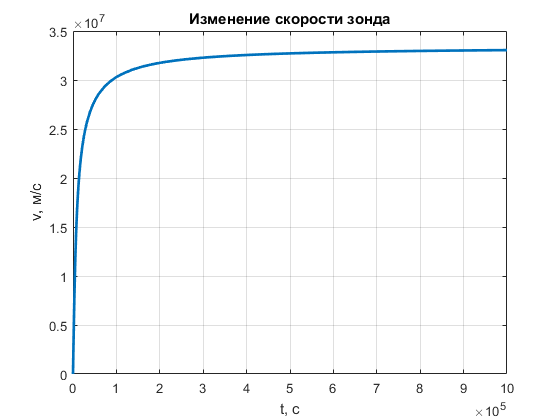
По рисунку видно, что большую часть энергии зонд получает, пока находится вблизи Земли — это связано с рассеиванием лазерного луча с расстоянием.

Функция v(t) не имеет предела в строгом смысле. Однако можно эмпирически показать, что ее значение на физически осмысленном промежутке времени не превышает 33000 км/с, что соответствует 40 годам в пути.

Вывод

С одной стороны, полученное значение лишь в два раза больше заявленного. Учитывая, что некоторые важные параметры модели были лишь предположениями, можно с уверенностью утверждать, что погрешность решения по абсолютной величине превосходит это различие. С другой стороны, для получения такого результата пришлось ввести множество упрощающих предположений, многие из которых недостижимы в реальности.

В любом случае это означает, что заявленный в Breakthrough Starshot порядок величины скорости достижим и не требует принципиально новых технологий.